Игра на математике

Проведение уроков с использованием дидактических игр, сказочных сюжетов, информационных технологий свидетельствует о стремлении учителей разнообразить жизнь школьника, вызвать интерес к познавательному общению, уроку, школе, удовлетворить потребность ребенка в развитии интеллектуальной, мотивационной, эмоциональной и других сфер.

Конечно, из таких уроков невозможно построить весь процесс обучения: они хороши лишь как разрядка, праздник для учащихся, однако каждому учителю необходимо найти место для подобных занятий в своей работе.

стараюсь наполнить уроки конкретными фактами, яркими образами и, сделав их более содержательными, разнообразными и занимательными, соединить математику с окружающим миром.

В работе по математике большое место занимают дидактические игры, то есть игры, содержание которых способствует развитию отдельных мыслительных операций, освоению вычислительных приемов, навыков в беглости счета. Целенаправленное включение игры в тот или иной вид работы повышает интерес детей к этой работе, усиливает эффект самого обучения. Создание игровой ситуации приводит к тому, что дети, увлеченные игрой, незаметно для себя и без особого труда и напряжения приобретают определенные знания, умения и навыки. Игра делает отдельные элементы по математике эмоционально насыщенными, вносит бодрый настрой в детский коллектив, помогает эстетически воспринимать ситуацию, связанную с математикой: красоту древней легенды, включающей задачу, драматизацию математического задания, наконец, стройность мысли при решении логической задачи.

Однако, несмотря на всю важность и значение игры в процессе работы по математике, она не самоцель, а средство для развития интереса к математике. Математическая сторона содержания игры всегда должна отчетливо выдвигаться на передний план. Только тогда она будет выполнять свою роль в математическом развитии детей и воспитании интереса их к математике.

В настоящее время общепризнанно, что усвоение знаний и формирование умений у детей будет более успешным, если проводить обучение в условиях, повышающих их мыслительную активность. С этой целью я использую дидактические материалы с ярко выраженной практической направленностью.

Например, в процессе изучения обыкновенных дробей можно использовать следующие занимательные упражнения:

1. Раздели яблоко на четырех друзей поровну. Какую часть яблока получит каждый друг? Обозначь эту часть дробью.

2. Отогни 1/4 часть картонного листа для изготовления коробки.

3. Отмерь для теста 2/3 стакана сахара.

4. Заполни литровую банку водой на указанную часть объема:

а) 1/3; б) 1/2; в) 2/3; г) 1/4; д) 3/4.

5. Отрежь от тесьмы длиной 1 метр 2/5 части. Какова длина отрезанной части тесьмы в сантиметрах?

6. На пакете с киселем написан способ приготовления: содержимое пакета нужно тщательно размешать в 1/2 стакана холодной воды. Затем, помешивая, влить 31/2 стакана горячей воды и довести до кипения. Вычислите, сколько всего стаканов воды потребуется для приготовления этого киселя.

Чтобы развить интерес у учащихся к математике, полезно использовать в учебном процессе занимательные задания для решения различных дидактических целей: активации имеющегося у учащихся опыта; повторения изученного материала; закрепления нового материала; обобщения, систематизации и дифференцировки знаний; выполнения самостоятельной работы и пр.

При изучении темы “Десятичные дроби” можно использовать игру “В мире животных”.

В нашей стране водится много бобров. Бобер — крупный грызун, ведет полуводный образ жизни, обитает по лесным рекам, сооружает плотины длиной 5—6 м. Ваша задача — узнать длину тела бобра (в дм). Вам поможет волшебный квадрат.

1. Из первой строки выберите наименьшее число.

2. Из второй строки выберите наибольшее число.

3. Из третьей строки — не наименьшее и не наибольшее число.

4. Найдите сумму выбранных чисел, и вы получите ответ на вопрос. 3,6 + 2,7 + 3,7 = 10 дм (длина бобра).

5. Сколько это см? Сколько м?

6. Сравните длину тела бобра со своим ростом.

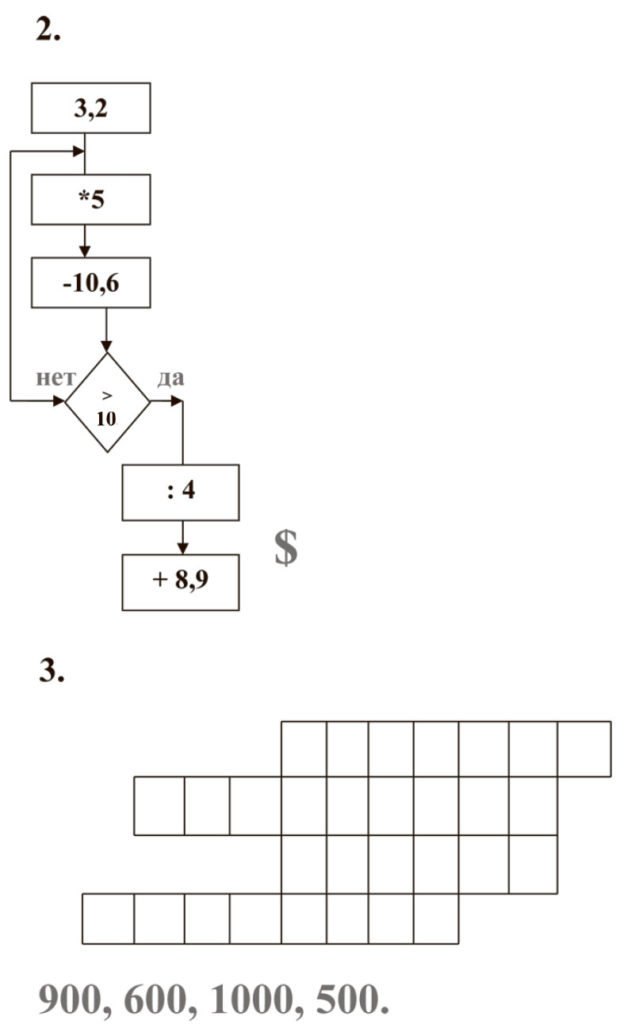
Очень ценятся мех и кожа бобра. Из жира бобра изготавливают лекарства. Узнайте, сколько стоит 100 г жира бобра. Ответить поможет вам блок-схема.

Бобер — отличный пловец и ныряльщик. Несколько минут он может находиться под водой.

1. В строки таблицы внесите названия чисел: 900, 600, 1000, 500.

2. В одном из столбцов прочитайте название числа, указав, сколько минут бобер может находиться под водой.

3. 5 мин — это сколько секунд?

4. Какую часть 5 минут составляет от 1 часа?

5,9	6,3	3,6
2,3	2,7	0
3,7	4,1	1,4

На земном шаре обитают птицы — безошибочные составители прогноза погоды на лето. Они из песка строят гнезда в форме усеченного конуса, в верхнем основании делают углубления, в которые откладывают яйца. Высота гнезда зависит от того, каким будет лето: сухим или дождливым. Если лето ожидается дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, если засушливым — то более низкими. Название этих птиц зашифровано примерами.

4,5:1,8; 3,15:0,15; 4,2:2,8; 36:0,08; 21:0,15; 60:2,5; 4,25:2,5; 490:14.

Заменив частные буквами, вы прочтете название птиц-метеорологов.

1,7	1,5	140	2,5	24	45	21	35
Г	А	И	Ф	Н	М	Л	О

Ответ: фламинго.

Можно ученикам предложить проанализировать математические идеи и термины, содержащиеся в произведениях известных писателей и поэтов.

Геометрия, 9 класс: Тема: “Окружность. Уравнение окружности”.

У лукоморья дуб зеленый,

Злотая цепь на дубе том,

И днем и ночью кот ученый

Всё ходит по цепи кругом.

Всем известны эти пушкинские строки. А задумывались ли вы над тем, какую линию описывает кот при своем движении?

Ответ: так как цепь всё время наматывается или сматывается с дуба так, что она натянута и образует касательные к окружности ствола, ее концы описывают линию, которая называется эвольвентой окружности; так что кот не зря назван Пушкиным ученым, он знаком с линией, изучаемой в вузе.

Математика, 6 класс. Тема: “Отношения и пропорции”.

Какое число зашифровано в этом стихотворении?

22 совы скучали

На больших сухих суках,

22 совы мечтали

О семи больших мышах,

О мышах довольно юрких

В аккуратных серых шкурках.

Слюнки капали с усов

У огромных серых сов.

Ответ: архимедово число, приблизительно равно 22/7.

Я считаю, что в процессе игры замечательный мир детства соединяется с прекрасным миром науки, в который вступают ученики. Различные знания и новые сведения ученик получает свободно. То, что на уроке казалось трудным, даже недостижимым, во время игры легко усваивается. Игра развивает детскую наблюдательность и способность определять свойство предметов, выявлять их существенные признаки. Таким образом, игры оказывают большое влияние на умственное развитие детей, совершенствуя их внимание, мышление, творческое воображение.

София НОВОГРОДСКАЯ,
учитель математики средней школы № 14 Лиды Гродненской области.
Фото Натальи КОЛЯДИЧ.