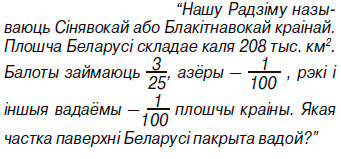Практыка-арыентаваная матэматыка

Пытанні развіцця і спалучэння розных форм і напрамкаў асноўнай і дадатковай адукацыі ў матэмытыцы і прыродазнаўчых навуках абмеркавалі ўдзельнікі ІІ Міжнароднай навукова-практычнай канферэнцыі “Бесперапынная арыентаваная адукацыя ў галіне матэматыкі і прыродазнаўчых навук: стан, развіццё, перспектывы”, якая прайшла ў анлайн-рэжыме і была арганізавана Мінскім абласным інстытутам развіцця адукацыі і Беларускім дзяржаўным універсітэтам. Педагогі падзяліліся эфектыўнымі напрацоўкамі арганізацыі навучання па матэматыцы, прадставілі ідэі стварэння інфармацыйнай адукацыйнай прасторы.

У інтэрактыўным асяроддзі

На думку настаўніка матэматыкі ліцэя № 1 Гродна Юрыя Уладзіміравіча Яўсейчыка, паток інфармацыі пад ціскам патрабаванняў сучаснага свету расце з году ў год, што абцяжарвае сучаснае абнаўленне падручнікаў і вучэбных дапаможнікаў, таму сучасную адукацыю без выкарыстання гаджэтаў у новых падыходах выкладання складана ўявіць.

Арганізацыя адукацыйнага працэсу з улікам павеваў сучаснасці на вучэбных занятках ажыццяўляецца шляхам выкарыстання асабістых смартфонаў навучэнцаў і настаўніка, а таксама бесправадной сеткі інтэрнэт установы адукацыі.

Стварэнне інтэрактыўнага адукацыйнага асяроддзя ажыццяўляецца па некалькіх напрамках. Па-першае, быў распрацаваны асабісты прадметны блог (http://2002math.blogspot.com.by) як крыніца інтэрактыўнага праграмнага матэрыялу. Такая інтэрактыўная пляцоўка выкарыстоўваецца для размяшчэння тэматычных відэаматэрыялаў, з дапамогай якіх навучэнцы могуць яшчэ раз азнаёміцца з тлумачэннем той ці іншай тэмы, пры гэтым маючы магчымасць праглядаць матэрыял патрэбную колькасць разоў да поўнага яго разумення; размяшчэння тэматычных прэзентацый; публікацыі мультымедыйных інтэрактыўных практыкаванняў, створаных у дадатку LearningApps.org і г.д.; размяшчэння электронных тэматычных тэстаў; публікацыі Google-форм, з дапамогай якіх праводзіцца рэфлексія ў рамках вучэбных заняткаў, ажыццяўляецца тэставы кантроль з наступнай апрацоўкай вынікаў з дапамогай дадатку Flubaroo. А таксама для размяшчэння дадатковага тэарэтычнага і практычнага матэрыялу; публікацыі дынамічных, інтэрактыўных стэрэаметрычных чарцяжоў; арганізацыі падрыхтоўкі вучняў да прадметнай алімпіяды, цэнтралізаванага тэсціравання; размяшчэння спасылак на карысныя праграмныя прадукты і інш.

Па-другое, была арганізавана работа навучэнцаў у інтэрнэт-рэсурсе “ЯКлас” (http://www.yaklass.by). “ЯКлас” дапамагае настаўніку праводзіць тэсціраванне ведаў навучэнцаў, задаваць дамашнія заданні ў электронным выглядзе. Для вучня гэта база электронных рабочых сшыткаў і бясконцы трэнажор па школьнай праграме. Дынамічныя рэйтынгі лідараў класа і школ дадаюць навучанню элементы гульні, якія стымулю­юць і школьнікаў, і настаўнікаў.

У межах трэцяга напрамку педагогам былі створаны дынамічныя, інтэрактыўныя стэрэаметрычныя малюнкі ў матэматычным пакеце GeoGebra — праграмным прадукце па распрацоўцы “жывых чарцяжоў” і рашэнні алгебраічных задач (https://www.geogebra.org). У гэтым дадатку дынамічныя чарцяжы выкананы да ключавых задач некаторых тэм геаметрычнага кампанента. Гэтыя малюнкі спрыяюць лепшаму бачанню прасторавага чарцяжа, а значыць, спрашчаюць працэс рашэння задачы. Акрамя гэтага, яны дазваляюць праглядаць этап пабудовы сячэнняў мнагаграннікаў плоскасцю на аснове аксіём і вывадаў з іх як у рэжыме відэа, так і ў зручным для навучэнца тэмпе прагляду.

Стварэнне інтэрактыўнага адукацыйнага асяроддзя дазваляе Ю.У.Яўсейчыку максімальна ўцягнуць навучэнцаў у адукацыйны працэс дзякуючы магчымасці аператыўнага доступу да рознага медыякантэнту, забяспеч­вае абмен інфармацыяй у рэжыме рэальнага часу, а таксама дае магчымасць наладзіць аператыўную зваротную сувязь.

Памочнік для вучняў і настаўнікаў

Настаўніцы матэматыкі сярэдняй школы № 16 Полацка Таццяна Міка­лаеўна Дзянісава і Святлана Анатольеўна Ананіч прадставілі вэб-рэсурс па прадмеце, распрацаваны педагогамі ўстановы, на якім размяшчаюцца вучэбныя матэрыялы, дапаможнікі, прэзентацыі ўрокаў, трэнажоры, тэсты і інш.

— Сучасны падыход да навучання школьнікаў на ўроках матэматыкі можа і павінен рэалізоўвацца з дапамогай інфармацыйных тэхналогій. Развіццё новага вучэбнага асяроддзя на базе інфармацыйна-адукацыйнай прасторы і магчымасцей, якія прадастаўляюцца IT-тэхналогіямі, дазволіць праз захапленне маладога пакалення электроннымі гаджэтамі і камп’ютарнай тэхнікай дасягнуць засваення ведаў і развіцця навыкаў у розных прадметных галінах, развіць творчыя здольнасці навучэнцаў, — лічыць Т.М.Дзянісава.

Вэб-рэсурс мае наступную структуру. На галоўнай старонцы размяшчаюцца раздзелы “Матэматыка ў класе”, “Матэматычныя турніры” і “Агульная інфармацыя аб сайце”. “Матэматыка ў класе” ўключае падзел прадмета па класах, а ў раздзеле “Агульная інфармацыя аб сайце” размешчаны звесткі аб настаўніку, ёсць кнопка “Звязацца” ў раздзеле зваротнай сувязі, пры націсканні якой педагогу прыходзіць апавяшчэнне, што наведвальнік хоча атрымаць кансультацыю.

Для кожнага класа былі распрацаваны асобныя раздзелы для спрашчэння карыстання сайтам. Націснуўшы на любы клас у раздзеле “Матэматыка ў класе”, карыстальнік трапляе на старонку класа, якая ўключае абавязковую спасылку на спампоўванне бясплатнага падручніка, а крыху ніжэй — наступныя раздзелы: “Тэарэтычны матэрыял”, “Урокі і прэзентацыі”, “Тэсты і трэніровачныя работы”. Першы раздзел уключае яркія кароткія канспекты па кожным параграфе падручніка, шпаргалкі асноўных тэм, формул, правіл і прыклады з падрабязным разборам рашэння, другі — відэаўрокі і прэзентацыі. Раздзел “Тэсты” дазваляе праверыць веды па неабходнай тэме. Запусціўшы тэст па той ці іншай тэме, карыстальнік перахо­дзіць на сайт канструктара тэстаў banktestov.ru для праходжання выбранага тэста. Раздзел “Трэніровачныя работы” змяшчае самастойныя і кантрольныя работы па тэме з прыкладамі для рашэння, падобнымі на тыя, што вучні рашалі ў класе, і больш складанымі, каб замацаваць практычную частку па прадмеце. Таксама на галоўнай старонцы ў раздзеле “Матэматыка ў класе” ёсць укладка “Дыдактычныя гульні”. Прайшоўшы па спасылцы, карыстальнік можа замаца­ваць пройдзены матэрыял у гульнявой форме: размаляваць размалёўку па тэме, замацаваўшы практычныя веды і ўменні, або пагуляць у матэматычнае лато, праверыўшы веданне тэарэтычнага матэрыялу.

Сайт цалкам аптымізаваны для мабільных прылад і зручны ў выкарыстанні. Ён па­дзелены на дзве асноўныя часткі: вэб-дадатак, з якім працуе карыстальнік, і дадатак для адміністратара, напісаны з выкарыстаннем Windows Forms.

— Рэсурс уяўляе сабой эфектыўны спосаб нефармальнага адукацыйнага ўзаема­дзеяння вучня і педагога, уцягвання навучэнцаў у самастойную вучэбную дзейнасць, — адзначае С.А.Ананіч. — Эфектыўнасць правядзення ўрока павышаецца за кошт памяншэння ролі класнай дошкі як асноўнага інструмента выкладання. Замест дошкі выкарыстоўваюцца магчымасці электронных сродкаў навучання: дэманстрацыі, дынамічныя малюнкі, якія дазваляюць паўтарыць тлумачэнне, звяртаючы ўвагу вучняў на моманты, якія выклікаюць цяжкасці. Урок-прэзентацыя дае магчымасць атрымання большага аб’ёму інфармацыі і заданняў за кароткі перыяд. Заўсёды можна вярнуцца да папярэдняга слайда або відэафрагмента (звычайная школьная дошка не можа змясціць той аб’ём, які можна размясціць на слайдах). Пры вывучэнні новай тэмы можна праводзіць урок-лекцыю з прымяненнем мультымедыйнай прэзентацыі або гатовых відэафрагментаў урока. Можна выкарыстоўваць прэзентацыю пры замацаванні матэрыялу для праверкі правільнасці выканання задання ўсімі вучнямі класа. Распрацаваны вэб-рэсурс можна прымяняць як на вучэбных занятках, так і па-за межамі школы.

З экалагічным зместам

Настаўніца матэматыкі сярэдняй школы № 6 Магілёва Святлана Віктараўна Крывёнак у сваёй рабоце выкарыстоўвае заданні экалагічнага зместу. Вопыт педагога грунтуецца на палажэннях тэорыі праблемнага навучання. Напрыклад, пры тлумачэнні тэмы “Складанне і адніманне дробаў з рознымі назоўнікамі” (5 клас) для пастаноўкі вучэбнай задачы педагог прапануе задачу з экалагічным зместам:

Для педагагічнай практыкі настаўніцы характэрны кампетэнтнасны падыход, сэнс якога ў стварэнні ўмоў для фарміравання вопыту самастойнага рашэння пазнавальных, камунікатыўных, маральных і іншых праблем, якія складаюць змест адукацыі. Напрыклад, для фарміравання вучэбна-пазнавальнай кампетэнцыі пры тлумачэнні правіла знаходжання працэнта ад ліку педагог прапануе навучэнцам для прагляду кароткі ролік аб праблеме знікнення лясоў на планеце. Затым дае наступную задачу: “У цяперашні час лясы на тэрыторыі Беларусі займаюць каля 166 тыс. км². Штогод гэтая велічыня памяншаецца на 2%. На колькі памяншаецца плошча лясоў за 1 год? Калі Беларусь застанецца без сваіх “лёгкіх”, калі гэты працэс не спыніць?”

Заданні з экалагічным зместам прымяняюцца на ўсіх этапах урока, для вывучэння матэрыялу па многіх тэмах. Так, на этапе замацавання ведаў настаўніца выкарыстоўвае задачы, якія рашаюцца колькасным метадам, задачы на міжпрадметныя сувязі. Напрыклад: “Беларусь называюць лёгкімі Еўропы. У нашай краіне балотамі (разам з асушанымі) занята 12% усёй плошчы. Знайдзіце плошчу “балотнага багацця” Беларусі” (тэма “Працэнты”, 6 клас). Пры адпрацоўцы вылічальных уменняў у 5—6 класах часта праводзіцца гульня “Лато”. Навучэнцы выконваюць дзеянні і супастаўляюць атрыманыя адказы з адпаведнымі часткамі карцінкі. У выніку атрымліваецца малюнак аб’екта, які знаходзіцца на тэрыторыі Беларусі. Пры фарміраванні вусных вылічальных навыкаў выкарыстоўваюцца заданні з ка­дзіраваным адказам. Напрыклад, пры вывучэнні тэмы “Задачы на прымяненне дробаў” (5 клас) навучэнцам прапануюцца прыклады, супастаўленне адказаў на якія прыводзіць да “раскадзіравання” праблемы, якая будзе абмяркоўвацца на ўроку.

У выніку такой работы у вучняў расце сярэдні бал па прадмеце, павышаецца матывацыя да вывучэння матэматыкі, высокая выніковасць і актыўнасць вучняў у матэматычных і экалагічных конкурсах рознага ўзроў­ню.

Для эфектыўнага ўрока

— Адным з матываў, які стымулюе цікавасць вывучэння таго ці іншага пытання курса матэматыкі, з’яўляецца яго практычная і прафесійная значнасць. Практыка-арыентаваныя задачы падтрымліва­юць гэтую цікавасць, — лічыць настаўніца матэматыкі Стайскай сярэдняй школы Лепельскага раёна Алена Казіміраўна Кулікова. — Практыка-арыентаваная задача — гэта сюжэтная задача, якая патрабуе ў сваім рашэнні рэалізацыі ўсіх этапаў метаду матэматычнага мадэлявання: фармалізацыі, перакладу прапанаванай задачы на мову матэматычных тэрмінаў (гэта значыць пабудовы матэматычнай мадэлі); рашэння задачы ўнутры мадэлі; інтэрпрэтацыі атрыманага рашэння (перакладу атры­манага выніку (матэматычнага рашэння) на мову, на якой была сфармулявана зыходная задача).

Пры вывучэнні школьнага курса геаметрыі педагог паказвае навучэнцам, што адны і тыя ж матэматычныя мадэлі (па сутнасці, вывучаныя азначэнні, уласцівасці, формулы і інш.) могуць быць выкарыстаны для вывучэння розных рэальных аб’ектаў. Такім чынам, можна пашырыць галіну прымянення атрыманых геаметрычных ведаў.

Напрыклад, вучням прапаноўваюцца задачы:

1. Лесвіца даўжынёй 5 м нахілена да сцяны дома. Вугал яе нахілу да паверхні Зямлі роўны 72°. Якой вышыні дасягае верхні канец лесвіцы?

2. Вугал пад’ёму пры ўзлёце самалёта роўны 30°. На якую вышыню паднімецца самалёт, праляцеўшы 500 м, калі вугал пад’ёму застанецца нязменным?

— Матэматычная мадэль умовы гэтых задач аднолькавая: па гіпатэнузе і вострым вугле прамавугольнага трохвугольніка вылічыць процілеглы катэт. Пры рашэнні гэтых задач навучэнцы, з аднаго боку, набываюць уменне знаходзіць у прамавугольным трохвугольніку па двух зададзеных элементах трэці, а з другога боку, пераконваюцца ва ўніверсальнасці матэматычных ведаў, — тлумачыць Алена Казіміраўна.

Выкарыстанне матывацыі ў выглядзе прыкладаў практычнага выкарыстання матэматычных фактаў дапамагае настаўніцы падводзіць вучня да ўсведамлення неабходнасці тэарэтычных ведаў: “Чаму матацыкл з каляскай стаіць на дарозе ўстойліва, а для матацыкла без каляскі неабходна дадатковая апора?”, “Чаму да садовай брамкі заўсёды прыбіваюць дыяганальную планку?”.

Педагог лічыць, што практыка-арыентаваныя задачы трэба выкарыстоўваць на ўсіх этапах навучання:

1) задачы або практычныя заданні для ўвядзення новых паняццяў і тэарэм (“Колькі каробак у форме прамавугольнага паралелепіпеда памерамі 30´40´50 (см) можна змясціць у кузаў машыны памерамі
2´3´1, 5 (м)?”);

2) нескладаныя задачы для першаснага замацавання матэрыялу (“Якая павінна быць плошча кабінета вышынёй 3,5 м для класа з 28 чалавек, калі на кожнага вучня трэба 7,5 м³ паветра?”);

3) больш складаныя задачы для ўключэння паняцця ў сістэму вядомых фактаў (“Зваршчыку неабходна вырабіць бак, які мае форму паралелепіпеда з асновай 1,4´2,2 м, каб ён змяшчаў 2 т вады. Якой павінна быць вышыня бака? (шчыльнасць вады — 1000 кг)”).

— Адна з цяжкасцей работы з практыка-арыентаванымі задачамі на ўроку заключаецца ў тым, што яны патрабуюць выдаткаў часу і інтэнсіўнай падрыхтоўкі настаўніка. Трэба ўмець прадбачыць магчымы ход заняткаў, каб быць гатовым да незвычайных сітуацый. Акрамя гэтага, трэба падабраць або распрацаваць задачы самому. Часу на гэта затрачваецца, вядома, шмат, але такія задачы павышаюць матывацыю і цікавасць навучэнцаў да прадмета і робяць урок больш эфектыўным. Таму значную частку практыка-арыентаваных задач уключаю ў праграму прадметнага гуртка па матэматыцы, — адзначае А.К.Кулікова.

Наталля КАЛЯДЗІЧ.
Фота аўтара.