Матэрыялы рэсурсу — для павышэння якасці геаметрычнай адукацыі навучэнцаў 8 класа

У чэрвені 2020 года мы, настаўнікі матэматыкі Рэчыцкай раённай гімназіі, — Ірына Уладзіміраўна Савіцкая, Святлана Уладзіміраўна Галаўко і Святлана Віктараўна Еўдачэнка, увайшлі ў склад творчай групы распрацоўшчыкаў матэрыялаў па геаметрыі за 8 клас для адзінага інфармацыйна-адукацыйнага рэсурсу. Больш як 10 месяцаў разам з асноўнай педагагічнай дзейнасцю мы асвойвалі працэс агучвання і відэамантажу, працавалі з рознымі графічнымі рэдактарамі, прыдумлялі ўласныя заданні, стваралі мадэлі для практыка-арыентаваных задач і рэалізоўвалі розныя ідэі па павышэнні якасці вывучэння геаметрыі.

Як настаўнікі-практыкі мы імкнуліся распрацаваць якасны адукацыйны прадукт у першую чаргу для навучэнцаў, але таксама прадугледжвалі выкарыстанне гэтага кантэнту ў далейшым і бацькамі на этапе кантролю або аказання дапамогі дзіцяці, і настаўнікамі на розных этапах урокаў, факультатываў і пазакласных мерапрыемстваў.

У навучэнцаў могуць быць розныя мэты выкарыстання матэрыялаў адзінага інфармацыйнага рэсурсу:

самастойнае вывучэнне новага вучэбнага матэрыялу ў выпадку пропуску ўрокаў або пры апераджальным навучанні;

карэкцыя ведаў у выпадку недастатковага засваення матэрыялу на ўроку;

абагульненне і сістэматызацыя раней атрыманых ведаў;

замацаванне і праверка атрыманых ведаў;

паглыбленне ведаў па ўжо вывучанай тэме.

У залежнасці ад мэт будзе ажыццяўляцца розны падыход да вывучэння матэрыялаў рэсурсу. Пры гэтым выконваецца адна з асноўных задач сучаснай адукацыі — навучыць здабываць веды. Настаўніку адводзіцца роля цьютара, які накіроўвае, каардынуе і адказвае на пытанні навучэнца. У навучэнца — галоўная роля: ён сам вызначае мэту свайго навучання, тэмп і аб’ём матэрыялу, усведамляе важнасць уласных намаганняў.

Якія этапы работы над тэмай асобнага модуля рэсурсу мы рэкамендуем? Незалежна ад мэты пачынаць лепш з раздзела “Вынік засваення тэмы”, у якім навучэнец вызначае крытэрыі паспяховасці засваення матэрыялу. Бацькі таксама могуць ажыццяўляць кантроль засваення ведаў навучэнцам, выкарыстоўваючы крытэрыі гэтага раздзела.

Далей варта пераходзіць да раздзела “Відэафрагмент з тлумачэннем новага матэрыялу”, у якім выкладаецца тэарэтычны матэрыял, прыводзяцца ўзоры рашэння задач рознага ўзроўню, дэманструюцца прыклады прымянення ведаў па тэме ў практычным жыцці. Калі навучэнец раней ужо вывучаў гэтую тэму, то ён зможа правесці карэкцыю, абагульненне і паглыбленне ведаў, выкарыстоўваючы прыведзеныя ў відэафрагменце метады рашэння базавых задач, задач павышанага ўзроўню складанасці, творчых і даследчых заданняў. Навучэнец выбірае зручны яму тэмп прагляду відэафрагмента, ставячы пры неабходнасці відэазапіс на паўзу і выконваючы пры гэтым заданні на доказ і вылічэнні ў сшытку.

Раздзел “Працуем з вучэбным дапаможнікам” рэкамендаваны тым, хто ўпершыню вывучае матэрыял модуля. У гэтым раздзеле ў далейшым будзе змяшчацца матэрыял вучэбнага дапаможніка па тэме, які навучэнцы змогуць выкарыстоўваць для замацавання вывучанага матэрыялу або ў якасці даведачнага дапаможніка.

Пры абагульненні, замацаванні і паглыбленні ведаў можна адразу перайсці да наступнага раздзела — “Правер сябе”, які змяшчае рознаўзроўневыя тэставыя заданні па тэме модуля. Пяты раздзел модуля “Дадатковыя матэрыялы” будзе напаўняцца зместам пазней.

Відэафрагмент з тлумачэннем новага матэрыялу пачынаецца з арганізацыйнага этапу, на якім задача настаўніка — дапамагчы навучэнцу эмацыянальна настроіцца на работу па вывучэнні новага матэрыялу. Так, у тэме “Тэарэма Піфагора” навучэнцы ў пачатку відэафрагмента знаёмяцца з часткай выказвання Іагана Кеплера аб тэарэме Піфагора: “Геаметрыя валодае двума скарбамі: адзін з іх — гэта тэарэма Піфагора…” Падкрэсліваецца значнасць гэтага матэрыялу ў рамках сусветнай навуковай спадчыны. Пры гэтым навучэнцы не застаюцца пасіўнымі слухачамі. Ім прапануецца знайсці ў сетцы інтэрнэт працяг выказвання і даведацца, што, на думку Кеплера, з’яўляецца другім скарбам і з чым параўноўваў гэтыя сусветныя дасягненні знакаміты вучоны. Навучэнцы бачаць партрэт Піфагора з фрэскі Рафаэля Санці “Афінская школа”, пры гэтым іх увага звяртаецца на тое, што фрагмент гэтай фрэскі адлюстраваны на вокладцы вучэбнага дапаможніка. Гэты прыём можа быць выкарыстаны настаўнікам і на ўроку.

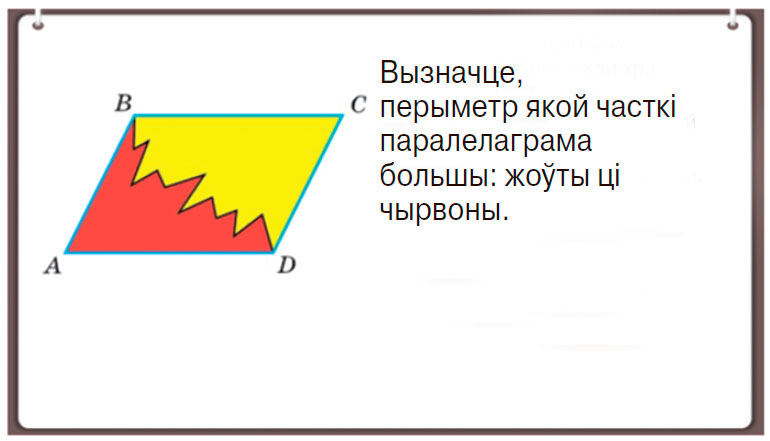
Наступны этап — матывацыйны, на якім навучэнцы бачаць пытанні для разгляду і вызначаюць вынік, да якога неабходна імкнуцца пры вывучэнні тэмы. На гэтым жа этапе навучэнцам прапануецца праблемная задача для павышэння цікавасці да тэмы, напрыклад, такая, як у модулі “Паралелаграм і яго ўласцівасці”.

На этапе актуалізацыі апорных ведаў і спосабаў дзеянняў у навучэнца з’яўляецца адчуванне віртуальных зносін з настаўнікам. Гэтаму спрыяюць заданні на запаўненне пропускаў, табліц, на адпаведнасць, на пошукі памылак, гульня “Веру — не веру”. Падобныя заданні могуць папоўніць метадычную скарбонку настаўніка матэматыкі.

Далей у відэафрагменце даецца тлумачэнне новага матэрыялу ў форме інтэрактыўнай гутаркі. Навучэнцу рэкамендуецца ў пэўныя моманты ставіць прайграванне відэа на паўзу і выконваць розныя заданні на доказы, вылічэнні або пабудовы ў сшытку, а затым звяраць свае вынікі з запісамі на экране. Настаўнік можа выкарыстоўваць на ўроку відэафрагмент на этапах тлумачэння і першаснага замацавання новага матэрыялу, робячы самастойную “агучку” і каментарый відэафрагмента, або рэкамендаваць навучэнцам матэрыял для работы па прынцыпе навучання “перавернуты клас”.

Многія матэрыялы змяшчаюць заданні па арганізацыі даследчай дзейнасці навучэнцаў і прадугледжваюць у далейшым індывідуальную, групавую або праектную работу. Напрыклад, пры вывучэнні тэмы “Плошча трапецыі” прапануецца вывесці формулу плошчы трапецыі пяццю рознымі спосабамі. У выніку навучэнцы атрымліваюць адну і тую ж формулу для знаходжання плошчы трапецыі, але пры гэтым паўтараюць формулы плошчаў іншых фігур і адчуваюць сябе творцамі геаметрычных формул і тэарэм. На ўроку гэтую работу зручней арганізоўваць у групах.

Матэрыялы відэафрагментаў прадугледжваюць дыферэнцыраваны падыход. Для высокаматываваных навучэнцаў прапануюцца заданні павышанага ўзроўню складанасці. Напрыклад, пры вывучэнні тэмы “Уласцівасць бісектрысы вугла трохвугольніка” дэманструецца рашэнне задачы з зорачкай з вучэбнага дапаможніка, у якой даказваецца ўласцівасць бісектрысы знешняга вугла трохвугольніка, пры гэтым разглядаецца толькі адзін выпадак размяшчэння бісектрысы знешняга вугла трохвугольніка. Навучэнцам прапануецца правесці ўласнае даследаванне і разгледзець усе астатнія выпадкі.

Каляндарна-тэматычнае планаванне не прадугледжвае вывучэнне на ўроках наступных тэм:

1. Цэнтральная і восевая сіметрыя.

2. Рашэнне задач па тэме “Плошчы многавугольнікаў”.

3. Рашэнне задач па тэме “Падобнасць многавугольнікаў”.

Гэта матэрыял модуляў 12, 18 і 24, які можа быць выкарыстаны ў рабоце з адоранымі навучэнцамі, пры падрыхтоўцы да алімпіяд і розных конкурсаў.

У відэафрагментах дэманструюцца анімацыйныя матэрыялы, якія могуць служыць асновай для арганізацыі дзейнасці навучэнцаў, накіраванай на развіццё творчых здольнасцей, на прымяненне атрыманых ведаў у практычным жыцці. Пасля візуалізацыі тэарэмы Піфагора навучэнцам можна прапанаваць стварыць уласныя мадэлі для дэманстрацыі таго, што плошча квадрата, пабудаванага на гіпатэнузе прамавугольнага трохвугольніка, роўная суме плошчаў квадратаў, пабудаваных на катэтах. Мадэлі можна напаўняць каменьчыкамі, фасоляй або крупамі.

Такім чынам, настаўнік арганізоўвае дзейнасць навучэнцаў па стварэнні ўласных творчых прадуктаў. Высокаматываваным навучэнцам, удзельнікам алімпіяднага руху можна прапанаваць даследчыя задачы на замошчванне квадратаў многавугольнікамі. Такія заданні заўсёды захапляюць навучэнцаў і прымушаюць усвядоміць, што матэматыка — гэта не сухая тэорыя, яна працуе ў рэальным жыцці, яе можна “ўбачыць, памацаць і адчуць”.

Асаблівае месца ў матэрыялах модуляў адводзіцца практыка-арыентаваным задачам і задачам на пабудову. Напрыклад, пры вывучэнні модуля “Рашэнне задач па тэме “Падобнасць многавугольнікаў” навучэнцы знаёмяцца з прапанаваным рашэннем і атрымліваюць заданне: знайсці іншыя спосабы рашэння ў сетцы інтэрнэт.

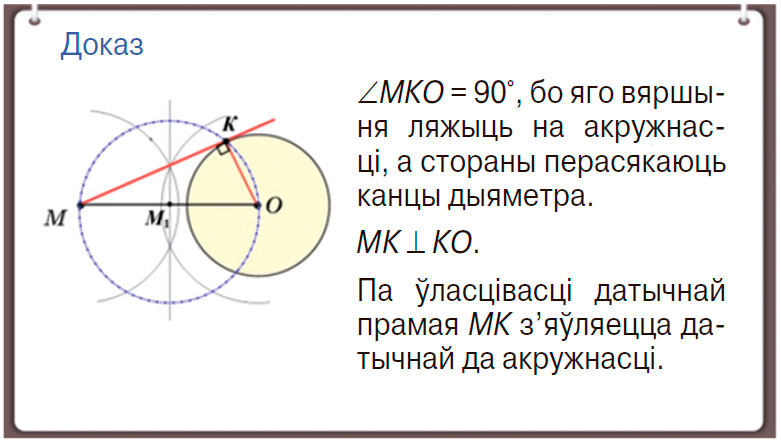
У матэрыялах модуляў прыводзяцца прыклады задач на пабудову з падрабязным афармленнем усіх этапаў: аналізу, пабудовы і доказу. Напрыклад, задача на пабудову датычнай да акружнасці з модуля 25 па тэме “Датычная да акружнасці”.

Таксама дэманструюцца задачы на пабудову, якія не патрабуюць падрабязнага афармлення, а прадугледжваюць прымяненне атрыманых ведаў у практычным жыцці. Такой з’яўляецца задача на дзяленне вугла напалову з дапамогай толькі лінейкі. Пры выкананні задання навучэнцы вучацца прымяняць на практыцы прымету ромба.

Пасля дэманстрацыі навучэнцам спосабу пабудовы вугла на мясцовасці, вядомага яшчэ старажытным егіпцянам, настаўнік можа прапанаваць выканаць практычную работу. У якасці “мясцовасці” можна выкарыстоўваць гумовыя дыванкі, у якасці калкоў — канцылярскія кнопкі-цвічкі.

Завяршаецца відэафрагмент выніковым этапам, на якім праводзіцца самаацэнка вынікаў вучэбнай дзейнасці. Навучэнцы вяртаюцца да матывацыйна-мэтавага этапу і правяраюць, ці атрымалі яны адказы на ўсе пастаўленыя спачатку пытанні. Калі не, то неабходна яшчэ раз вывучыць матэрыял відэафрагмента. Пры станоўчым адказе рэкамендуецца замацаваць атрыманыя веды пры выкананні тэставых заданняў. Дапушчальны час для відэафрагментаў, прызначаных для навучэнцаў 8 класа, 10—12 мінут. На выніковым этапе ў відэафрагментах дэманстраваўся апорны канспект, у якім у кароткай форме прыводзіліся ўсе тэарэтычныя матэрыялы па тэме.

У заключэнне навучэнцам даюцца заданні на пошук пазнавальнай інфармацыі ў сетцы інтэрнэт. Напрыклад, даведацца, як звязаны геаметрычная фігура ромб і музычны інструмент бубен.

Матэрыялы адзінага інфармацыйна-адукацыйнага рэсурсу дазваляюць арганізаваць самастойную работу навучэнцаў па самаадукацыі і даць магчымасць адчуць радасць поспеху ад уласных адкрыццяў і перамог. Спадзяёмся, што праведзеная намі работа будзе карысная калегам, навучэнцам і іх бацькам і будзе служыць высокай мэце павышэння якасці геаметрычнай адукацыі ў нашай краіне.

Ірына САВІЦКАЯ,
настаўніца матэматыкі Рэчыцкай раённай гімназіі.