Пазнанне лічбамі

Не абавязкова быць настаўнікам матэматыкі, каб зразумець, што першасныя навыкі аднімання, складання, дзялення і множання немагчыма засвоіць без гульні. Канечне, гульня на ўроку — гэта не забаўка ў чыстым выглядзе, але разнастайныя задачы і практыкаванні займальнага характару, якія патрабуюць праяўлення знаходлівасці, кемлівасці, арыгінальнасці мыслення, умення крытычна ацаніць умовы або пастаноўку пытання, дзецям вельмі падабаюцца. А калі ў працэсе такой гульні набываюцца неабходныя матэматычныя ўменні (а гэта найперш вылічэнні), то задаволенымі застануцца ўсе: і навучэнцы, і настаўнікі.

Хутка летнія канікулы. Зразумела, усе іх чакаюць з нецярпеннем. Але, як правіла, пасля першага канікулярнага месяца хочацца мазгавога штурму, а школы закрыты. І тут вельмі дарэчы будзе звярнуцца да гульні. Мікалай Пятровіч Лявонаў з’яўляецца своеасаблівым вынаходнікам розных матэматычных гульняў, яго матэматычны квадрат вядомы далёка за межамі нашай краіны. “Стаць цуда-дзіцем вельмі проста. Матэматычны квадрат — наглядны дапаможнік для практыкі ў складанні, адніманні, множанні і дзяленні. Дзеці лепш разумеюць і запамінаюць лічэнне, калі бачаць працэс складання або аднімання.
На гэтым квадраце можна перарашаць мільярд прыкладаў, проста перастаўляючы шашкі, нічога не запісваючы на паперы. Гэта развівае памяць і разуменне. Любую інфармацыю можна сістэматызаваць так, каб дзіця спазнавала навуку з цікавасцю і лёгкасцю. Матэматычны квадрат складзены менавіта па гэтым прынцыпе. Яго можна выкарыстоўваць і як поле для гульні, спаборніцтваў”, — расказаў Мікалай Пятровіч.
Дарэчы, вынаходства квадрата Мікалай Пятровіч запатэнтаваў, пацвердзіўшы яго ўнікальнасць. Гэты квадрат з поспехам выкарыстоўваюць юныя шахматысты сталіцы, для якіх, як вядома, матэматычныя вылічэнні, даведзеныя да аўтаматызму, — аснова поспеху. Матэматычныя гульні М.П.Лявонава зацікавілі і прафесійных матэматыкаў. У прыватнасці, А.В.Пракапчук, малодшы навуковы супрацоўнік Інстытута матэматыкі НАН Беларусі, кандыдат фізіка-матэматычных навук, аналізуючы гульню Лявонава “Экзамен”, адзначыў, што яна з’яўляецца добрым дапаможнікам для вывучэння правіл арыфметычных дзеянняў над лікамі.

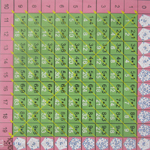
Вучэбная гульня “Экзамен” уяўляе сабой квадрат 11×11 з лічбамі ў кожным квадраце. Асноўнае поле гульні — унутраны квадрат 9×9 зялёнага колеру, а па перыметры размешчаны чырвоныя квадраты. Пры гэтым на квадратным полі праведзены дыяганальныя стрэлкі (адна стрэлка ідзе па галоўнай дыяганалі, а іншыя — паралельныя пабочнай дыяганалі).
У зялёных квадратах напісана сума двух лікаў (напрыклад, 5+3), пад ёй здабытак гэтых жа лікаў (напрыклад 15). Для вызначэння выніку складання двух лікаў меншых за 10 прапануецца знайсці клетку з паказаным складаннем на ёй і ўздоўж пабочнай дыяганалі прайсці да чырвонага квадрата, які змяшчае адказ.
У кожным зялёным квадраце, акрамя ўказання складання, ёсць лічба, якая паказвае вынік множання гэтых жа лічбаў. Для навучання множанню аўтар прапануе закрываць ніжнюю частку квадрата і толькі пасля агучвання ўласнага адказу звяраць яго з лікам на полі. Такім чынам, на полі гульні “Экзамен” ёсць табліцы і складання, і множання.
З дапамогай гэтай табліцы можна праводзіць і адніманне з дзяленнем. Для аднімання трэба стартаваць з чырвонага квадрата (памяншаемае) і ісці ўверх па дыяганалі на столькі клетак, колькі трэба адняць, і нумар радка будзе рознасцю. Для дзялення трэба знайсці дзель у адным з зялёных квадратаў, дзельнік будзе адным з лікаў сумы ў гэтым жа квадраце, прыватнае — іншы лік гэтай сумы. На адвароце апісаны правілы па знаходжанні вынікаў усіх чатырох арыфметычных дзеянняў.

На адвароце таксама даюцца правілы гульні “Магічны квадрат”. Поле для гэтай гульні і гульні “Экзамен” супадаюць. Сутнасць у тым, каб пасля таго, як былі выкінуты дзве косткі, як мага хутчэй паставіць адну з костак на месца складання лікаў, што выпалі, а другую — на месца з вынікам гэтага складання і пляснуць у далоні.
“Гульня ў цэлым стымулюе вывучэнне правіл складання, мінусам з’яўляецца тое, што пры кіданні звычайных костак задзейнічана не ўсё поле для гульні. Можна прапанаваць выкарыстоўваць косткі з вялікай колькасцю граней. Тым не менш апісаныя вышэй гульні з’яўляюцца наглядным дапаможнікам для вывучэння табліц складання і множання (а таксама аднімання і дзялення). Думаю, што пасля выпраўлення заўваг прапанаваныя гульні можна ўкараніць у вучэбны працэс”, — заўважыў А.В.Пракапчук.
Ёсць у арсенале вынаходніка М.П.Лявонава развіццёвая гульня “Зорачкі”. Яна можа дапамагчы дзіцяці замацаваць навыкі складання і аднімання лікаў (адзінкі, дзясяткі, сотні). Для правядзення гульні на стале ўкладваюцца зорачкі, пры гэтым правая будзе паказваць значэнне адзінак, сярэдняя — дзясяткаў, левая — соцень. На канцах зорачак пазначаны лічбы ад 0 да 9 уключна. Падчас гульні варта звяртаць увагу на лічбу на верхнім промні зорачкі. Далей на стале трэба ўсталяваць форму для зорачак. Тры зорачкі размясціце зверху, пры гэтым першапачаткова на верхнім промні зорачак усталёўваецца нуль.

Прыклад.
Кідаем кубік першы раз. Ён паказвае 6 кропак. Устаўляем у крайнюю правую форму зорачку адзінак з лічбай 6 на верхнім промні. Кідаем кубік другі раз. Ён паказвае 5 кропак. Устаўляем у сярэдзіну формы зорачку дзясяткаў з лічбай 5 уверсе. У выніку атрымаўся лік 56.Форму паднімаем і пераносім на свабоднае месца, зорачкі застаюцца на сваім месцы.
Кідаем кубік трэці раз, ён паказвае 3 кропкі. Вусна робім складанне для зорачкі адзінак: 6 +3 = 9. Устаўляем зорачку адзінак з лічбай 9 у форму на сваё месца справа. Кідаем кубік зноў, бачым 5 кропак. Робім складанне для зорачкі дзясяткаў: 5  +5 = 10. Устаўляем гэтую зорачку з лічбай 0 на верхнім промні ў сярэдзіну формы, а трэцюю зорачку соцень з лічбай 1 — у крайнюю левую форму. У выніку можна прачытаць новы лік: 109. Далей зноў пераносім форму на вольнае месца і, кідаючы кубік, робім вылічэнні. Аналагічна можна замацаваць адніманне, але для гэтага першапачаткова варта на зорачках усталяваць на верхнім промні лічбу 9.

Яшчэ прыклад.
Першапачаткова зорачкі паказваюць лік 999. Кідаем кубік, ён паказвае 3 кропкі. Вусна робім адніманне для зорачкі адзінак: 9-3 = 6. Устаўляем гэтую зорачку ў самую правую форму з лічбай 6 на верхнім промні. Кідаем кубік другі раз, ён паказвае 5 кропак. Аднімаем для зорачкі дзясяткаў: 9-5 = 4. Устаўляем у сярэднюю форму зорачку з лічбай 4. Кідаем кубік трэці раз, бачым 4 кропкі, аднімаем для зорачкі соцень: 9-4 = 5. Устаўляем у левую форму гэтую зорачку з лікам 5. У выніку ўсе тры зорачкі паказваюць лік 546.
Зноў кідаем кубік, ён паказвае лічбу 4. Лічым для зорачкі адзінак: 6-4 = 2. Устаўляем у правую форму зорачку з лічбай 2. Зноў кідаем кубік, ён паказвае 5 кропак. Варта зрабіць адніманне для зорачкі дзясяткаў: 4-5, але гэта немагчыма, таму ўяўляем, што 1 дзясятак забіраем у трэцяй зоркі — зорачкі соцень: 5-1 = 4. Устаўляем у левую форму зорачку з лічбай 4 і далей робім адніманне для зорачкі дзясяткаў: 14-5 = 9. У сярэднюю форму ставім зорачку з лічбай 9. У выніку атрымліваем лік 492. Гульня можа быць працягнута.
Ёсць у Мікалая Пятровіча і “Зорны калькулятар”, які ў стане замяніць звычную для нас вылічальную машыну. Дзесяць зорачак навучаць вас лічыць ад аднаго да дзевяці мільярдаў дзевяцьсот дзевяноста дзевяці мільёнаў дзевяцьсот дзевяноста дзевяці тысяч дзевяцьсот дзевяноста дзевяці. А таксама рабіць такія арыфметычныя дзеянні, як складанне, адніманне, дзяленне, множанне, узвядзенне ў ступень і веданне квадратнага кораня.

Прэзентуючы свае гульні, Мікалай Пятровіч заўсёды звяртае ўвагу на тое, што арыфметыка служыць пазнанню велічыні інфармацыі, якая вас цікавіць, лічбамі.
Як сведчаць шматлікія крыніцы, лічэнне прадметаў на самых ранніх ступенях развіцця чалавечага грамадства прывяло да стварэння самых простых паняццяў арыфметыкі натуральных лікаў. На аснове распрацаванай сістэмы вуснага лічэння ўзнікаюць пісьмовыя сістэмы лічэння і паступова выпрацоўваюцца прыёмы выканання над натуральнымі лікамі чатырох арыфметычных дзеянняў.
Патрэбы вымярэння самыя розныя. Гэта і колькасць збожжа, даўжыня шляху і г.д. — прыводзяць да з’яўлення назваў і абазначэнняў простых дробавых лікаў і да распрацоўкі прыёмаў выканання арыфметычных дзеянняў над дробамі. Такім чынам, назапашваецца матэрыял, які паступова складаецца ў найстаражытнейшую матэматычную навуку — арыфметыку.

Вымярэнне плошчаў і аб’ёмаў, патрэбы будаўнічай тэхнікі, а потым — астраноміі, даюць старт развіццю пачатковай геаметрыі. Гэтыя працэсы ішлі ў многіх народаў у значнай меры незалежна і паралельна. Асаблівае значэнне для далейшага развіцця навукі мела назапашванне арыфметычных і геаметрычных ведаў у Егіпце і Вавілоніі.
У Вавілоніі на аснове развітой тэхнікі арыфметычных вылічэнняў з’явілася пачатковая алгебра, а ў сувязі з запытамі астраноміі — пачатковая трыганаметрыя. Старажытнаегіпецкія матэматычныя тэксты першай паловы ІІ тысячагоддзя да н. э. складаюцца ў пераважнай большасці з прыкладаў на рашэнне асобных задач.
Матэматычнай тэорыі ў сэнсе доказаў агульных тэарэм, магчыма, зусім не існавала, таму гаварыць можна менавіта аб рэцэптах для рашэння некаторых тыпаў задач. Пра гэта сведчыць, напрыклад, тое, што дакладныя рашэнні выкарыстоўваліся без усялякага адрознення ад прыблізных. Тым не менш высокая будаўнічая тэхніка, складаныя зямельныя адносіны, дакладны егіпецкі каляндар з’яўляюцца сведчаннямі матэматычных фактаў.
А матэматычныя гульні М.П.Лявонава могуць дапамагчы стварыць уласную матэматычную біяграфію ці скласці сямейны бюджэт.
“Гэты матэматычны квадрат дапаможа лічыць вашы даходы і выдаткі. Напрыклад, вам трэба даведацца, колькі неабходна сродкаў для забеспячэння вашай жыццядзейнасці. Квадрат падзелены на зоны: харчаванне, вольны час, банкаўскія зберажэнні і інш. Ставячы шашкі на лічбы, вы будзе бачыць, колькі і на што вы траціце і ці эфектыўныя гэтыя выдаткі.
Вы ведаеце, што ў месяц на цыгарэты ў вас ідзе, напрыклад, 30 долараў. Памножыўшы гэты лік на 12 месяцаў, атрымаеце 360 долараў выдаткаў у год. Быццам бы нямнога. А што, калі падлічыць, колькі часу вы марнуеце на куплю цыгарэт?
Калі вы купляеце іх тры разы на тыдзень, затрачваючы на кожны выхад у магазін 20 хвілін, то за год атрымліваецца 48 гадзін, а гэта 7 шасцігадзінных працоўных дзён. Гэта значыць, у год чалавек марнуе працоўны тыдзень на куплю цыгарэт і яшчэ сам гэтую “работу” і аплачвае”, — адзначыў вынаходнік.
Па меркаванні Мікалая Пятровіча, яго гульні маюць яшчэ і выхаваўчы аспект, бо вучаць дзяцей працаваць самастойна, прычым робяць гэта гуляючы.

Вольга ДУБОЎСКАЯ.
Фота аўтара.