Універсальнага падыходу не бывае

Як арганізаваць дыферэнцыраванае навучанне?

Настаўніца матэматыкі сярэдняй школы № 157 Мінска імя А.С.Бурдзейнага, фіналістка Рэспубліканскага конкурсу прафесійнага майстэрства педагагічных работнікаў “Настаўнік года Рэспублікі Беларусь — 2017”, член клуба настаўнікаў Мінска “Вялікі перапынак” Таццяна Іванаўна Рычак запрасіла да сябе на ўрок у 8 клас па тэме “Сярэдняя лінія трохвугольніка”. Нягледзячы на тое, што заняткі пачыналіся ў 8 гадзін раніцы, ніхто з вучняў не спазніўся, усе былі бадзёрымі і засяроджанымі.

У чаканні званка мы размаўлялі з Таццянай Іванаўнай. Яна расказала, што пасля заканчэння механіка-матэматычнага факультэта БДУ першыя гады работы ў школе самым складаным для яе было арганізаваць з класам этап замацавання вучэбнага матэрыялу. Інтуітыўна яна адчувала, што выконваць з усімі дзецьмі аднолькавыя заданні нельга, трэба даваць магчымасць кожнаму працаваць на сваім узроўні, у сваім тэмпе, а значыць, неабходна дыферэнцыраваць вучэбны працэс. Падчас урока яна прадэманстравала, як ажыццявіць гэта на практыцы.

“Вітаю вас, паважаныя вучні, рада бачыць вас. Пачынаем наш урок з разбору дамашняга задання. Адкрываем рабочыя сшыткі. Ці ёсць у вас пытанні да мяне? — звяртаецца да васьмікласнікаў Таццяна Іванаўна. — Мяркую, што са 102 і 105 задачамі вы павінны былі справіцца самастойна, а вось са 107 маглі ўзнікнуць цяжкасці. Умовы задачы наступныя: “У трохвугольніка праведзены тры сярэднія лініі, якія падзяляюць яго на чатыры трохвугольнікі. Трэба даказаць, што яны роўныя”. Настаўніца зрабіла адпаведны чарцёж на дошцы. Свае тлумачэнні дала Кацярына. Такім чынам, у скарбонку ведаў дзяцей пра сярэднюю лінію трохвугольніка трапіла яшчэ адна яе ўласцівасць: сярэдняя лінія трохвугольніка падзяляе яго на чатыры роўныя часткі.

Вучні запісалі ў дзённік дамашняе заданне (важна зрабіць гэта ў пачатку ўрока), у якім былі абавязковыя для выканання нумары і адно заданне для цікаўных. У сшытках пазначылі дату і тэму ўрока — “Сярэдняя лінія трохвугольніка”. Таццяна Іванаўна разам з вучнямі фармулюе мэты і задачы ўрока: замацаваць паняцце сярэдняй лініі трохвугольніка, яе ўласцівасці і прыкметы і навучыцца рашаць задачы з іх прымяненнем.

Каб паспяхова рашаць задачы па геаметрыі, неабходна добра ведаць тэорыю. Настаўніца выклікае па чарзе дзяцей і задае ім пытанні: “Што такое сярэдняя лінія трохвугольніка?” (адрэзак, які спалучае сярэдзіны дзвюх старон), “Колькі сярэдніх ліній можна пабудаваць у трохвугольніку?” (тры), “У якой фігуры яшчэ можна пабудаваць сярэднюю лінію?” (у чатырохвугольніку), “Чым адрозніваецца сярэдняя лінія ад медыяны?” (медыяна злучае сярэдзіну стараны і вяршыню трохвугольніка, а сярэдняя лінія толькі сярэдзіну старон), “Якія ўласцівасці сярэдняй лініі?” (яна паралельная аснове і роўная яе палове).

“Для замацавання тэорыі папрацуем з простымі задачамі, — працягвае Таццяна Іванаўна. — Сярэдняя лінія трохвугольніка роўная 4. Чаму роўная аснова, паралельна якой праведзена сярэдняя лінія? (Аснова роўная 8.) Старана трохвугольніка — 10 см. Чаму роўная сярэдняя лінія, якая праведзена паралельна старане? (Адказ: 5.) Перыметр трохвугольніка, які пабудаваны з сярэдніх ліній, роўны 10. Чаму роўны перыметр вялікага трохвугольніка? (Адказ: 20.) Перыметр вялікага трохвугольніка — 30 см. Чаму роўны перыметр маленькага трохвугольніка, пабудаванага з сярэдніх ліній? (Адказ: 15.) Абагульнім, як звязаны перыметр трохвугольніка і перыметр трохвугольніка з сярэдніх ліній. Так, перыметр трохвугольніка з сярэдніх ліній у 2 разы меншы, чым перыметр вялікага трохвугольніка. Калі правесці ўсе тры сярэднія лініі ў трохвугольніку, то яны адсякуць 4 роўныя трохвугольнікі. А зараз вазьміце лісцікі з матэматычным дыктантам (тэстам), якія ляжаць у вас на партах, падпішыце прозвішча, варыянт і пачынайце рашаць”.

Пакуль дзеці пішуць тэст, які адначасова выводзіцца на вялікі экран, настаўніца ходзіць па класе, заглядвае ў сшыткі вучняў і агучвае некаторыя парады-каментарыі, спыняецца каля тых, у каго ўзніклі цяжкасці.

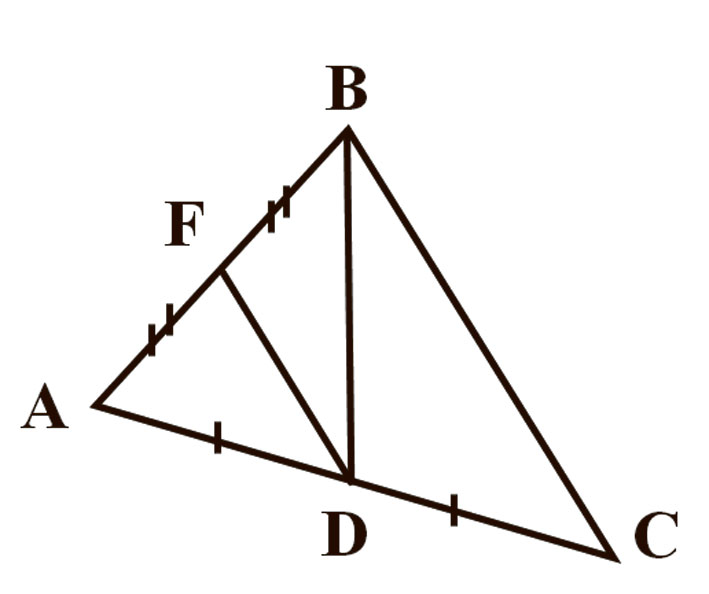
Мал. 1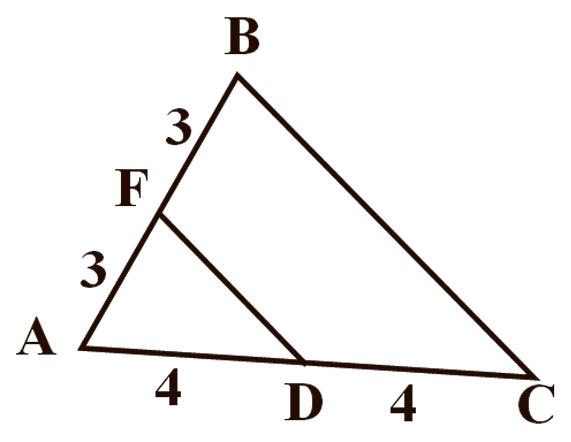
Мал. 2
Мал. 3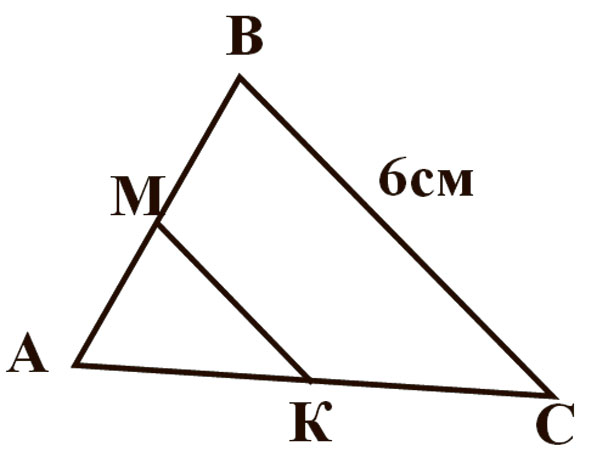
Мал. 4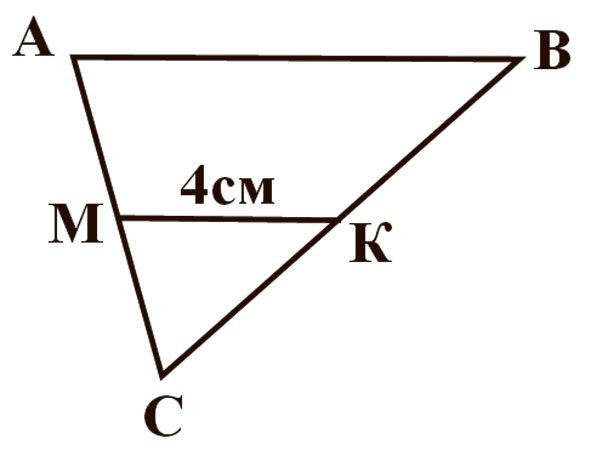
Мал. 5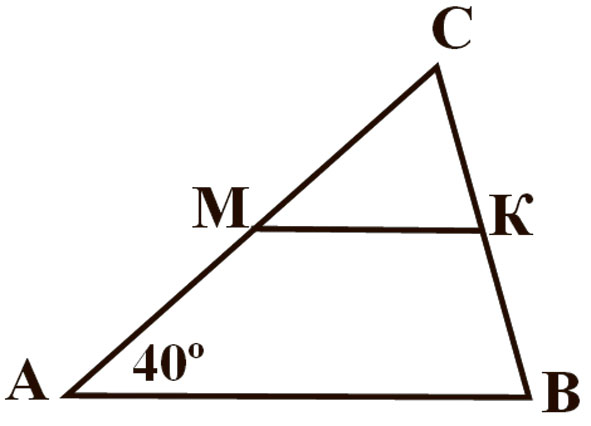
Мал. 6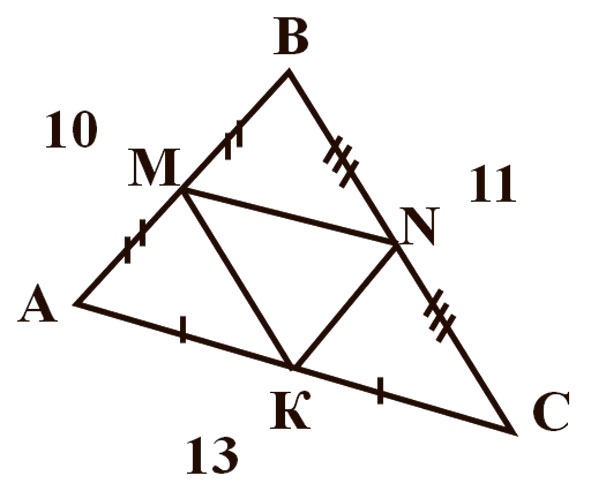
Мал. 7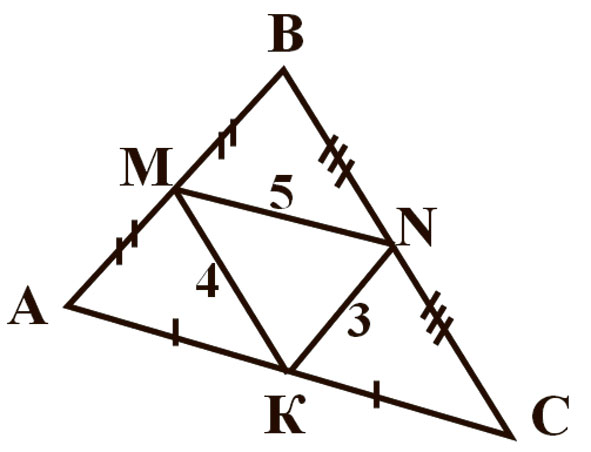
Мал. 8

Пытанні тэста ў першым варыянце наступныя: 1. Закончыце фразу: адрэзак, які злучае сярэдзіны дзвюх старон трохвугольніка, называецца… 2. Пазначыць адрэзак, які з’яўляецца сярэдняй лініяй. (Гл. малюнак 1.) 3. Ці з’яўляецца адрэзак на чарцяжы сярэдняй лініяй? (Гл. малюнак 2.) 4. Калі МК — сярэдняя лінія, то СМ=? (Гл. малюнак 3.) 5. МК — сярэдняя лінія. Знайсці МК. (Гл. малюнак 4.) 6. МК — сярэдняя лінія. Знайсці АВ. (Гл. малюнак 5.) 7. МК — сярэдняя лінія, знайсці вугал СМК. (Гл. малюнак 6.) 8.Знайдзіце перыметр трохвугольніка MNK. (Гл. малюнак 7.) 9. Знайдзіце перыметр трохвугольніка ABC. (Гл. малюнак 8.) 10. Сярэдняя лінія раўнабедранага трохвугольніка паралельная аснове і роўная 5 см. Знайдзіце стораны трохвугольніка, калі яго перыметр роўны 28 см (трэба пазначыць даўжыні трох старон трохвугольніка).

“Зверым адказы. Для гэтага памяняйцеся, калі ласка, сваімі работамі і праверце адно аднаго, — гаворыць педагог. — Калі адказ няправільны, закрэсліце яго і напішыце правільны, калі правільны — пастаўце плюсік. У каго ў тэсце было 2 памылкі і больш, падыміце, калі ласка, руку. Якія ў вас былі цяжкасці?” Вучням, якія дапусцілі адну памылку або ўсё напісалі правільна, настаўніца ўручае папяровыя медалі з надпісам “Малайчына, так трымаць!”. Падводзячы вынік гэтага этапу, Таццяна Іванаўна адзначае, што тэст быў складзены такім чынам, каб максімальны бал, які можна было за яго атрымаць, складаў 6 балаў, а гэта сярэдні ўзровень ведаў. “Каго задавальняе “шасцёрка”, на перапынку падыдзіце да мяне з дзённікам. Калі ж вы далей будзеце добра працаваць на ўроку, то зможаце павысіць сваю адзнаку. Пераходзім да наступнага этапу — рашэння задач, — гаворыць педагог. — Прапаную выканаць творчае заданне, якое прымножыць вашы тэарэтычныя веды пра сярэднюю лінію трохвугольніка. Кожны рад будзе выконваць сваё заданне. Вучні першага рада павінны знайсці адказ на пытанне “Вяршынямі якой фігуры з’яўляюцца сярэдзіны старон любога выпуклага чатырохвугольніка?”. Другі рад разважае, вяршынямі якой фігуры з’яўляюцца сярэдзіны старон ромба. Трэці рад вырашае, вяршынямі якой фігуры з’яўляюцца сярэдзіны старон прамавугольніка. Трэба не толькі намаляваць фігуры, але і абгрунтаваць, чаму атрымалася пэўная фігура. Працаваць можна ў групах, дапамагаючы адно аднаму. У сваю чаргу ўпэўнена, што вам спатрэбіцца і мая дапамога, таму я таксама папрацую каля дошкі”.

У першага рада пры спалучэнні сярэдзін чатырохвугольніка атрымліваецца паралелаграм. Чаму? Паралелаграм, які атрымліваецца пры злучэнні сярэдзін старон адвольнага чатырохвугольніка, называецца паралелаграмам Варыньёна (у гонар французскага матэматыка П’ера Варыньёна, які даказаў гэты геаметрычны факт). Другі рад працуе з ромбам, і ў выніку спалучэння яго сярэдзін атрымліваецца прамавугольнік. Вучні даказваюць гэты факт. У трэцяга рада ў выніку спалучэння сярэдзін прамавугольніка атрымліваецца ромб.

Пасля непрацяглай фізкультхвілінкі вучні прыступаюць да самастойнай работы. Тыя, хто добра справіўся з папярэднім матэматычным дыктантам, пачынаюць рашаць задачы з чарцяжамі (на 7—10 балаў), якія настаўніца прымацавала на адваротны бок папяровых медалёў. З тымі, хто не вельмі добра выканаў тэст, настаўніца працуе асобна.

7—8 балаў	Стораны трохвугольніка адносяцца як 10:8:4. Злучыўшы сярэдзіны ўсіх старон, атрымаем трохвугольнік з перыметрам 88 см. Знайдзіце стораны гэтага трохвугольніка	Падказка: пазначыць стораны дадзенага трохвугольніка з дапамогай зменнай і скласці ўраўненне для трохвугольніка з перыметрам 88см. Адказ: 80см, 64см, 32см
9—10 балаў	Медыяна прамавугольнага трохвугольніка, праведзеная з вяршыні прамога вугла, роўная 6 см. Знайдзіце адрэзак, які злучае сярэдзіны катэтаў	Падказка: успомніць уласцівасць медыяны, праведзенай з вяршыні прамога вугла. Чаму яна роўная? Глядзець тэму: паралелаграм і яго ўласцівасці. Адказ: 6 см
Калі рашылі задачы, то выканаць № 110 (а) з падручніка

Урок заканчваецца, настаўніца правярае задачы. У якасці рэфлексіі яна прапаноўвае дзецям паразважаць пра сваё месца ў жыцці. Для гэтага трэба намаляваць трохвугольнік, сярэднюю лінію і вызначыць сваё месца на ёй з дапамогай смайліка (на сярэдняй лініі, вышэй або ніжэй за яе). Звініць званок, вучні падыходзяць да Таццяны Іванаўны з дзённікамі.

“Восьмы клас, у якім сёння праходзіў урок, перадпрофільны. Для вучняў гэтага класа праводзяцца факультатыўныя заняткі па фізіцы і матэматыцы, а таксама прадастаўляюцца платныя паслугі па гэтых прадметах. Сённяшні ўрок-замацаванне даказаў, што ўсе вучні засвоілі праграмны матэрыял у асноўным на дастатковым узроўні. Мэта ўрока дасягнута, — адзначыла Таццяна Іванаўна. — Асобныя вучні рашалі задачы на высокім узроўні. Урок быў насычаным, праходзіў у добрым тэмпе, за 45 мінут мы многае паспелі зрабіць. На занятках я правяла матэматычны дыктант, які дазволіў праверыць у вучняў не толькі тэорыю, але і яе разуменне (практыку). Гэты тэст разлічаны на максімальны бал — 6. З яго дапамогай я правяла дыферэнцыяцыю ведаў дзяцей, высветліла, хто на якім узроўні знаходзіцца, каб з улікам гэтага тлумачыць матэрыял. Каб сэканоміць час і больш увагі ўдзяліць рашэнню задач, я загадзя падрыхтавала сродак нагляднасці (чарцяжы). Па выніках тэста вучні, якія з ім справіліся, прадоўжылі працаваць самастойна, а хто не справіўся, працаваў са мной. У выніку за ўрок 6 балаў ніхто не атрымаў, 7 балаў атрымалі 6 чалавек з класа, планку ў 9—10 балаў адолелі двое. Асноўная адзнака ў класе — “8”.

“Класы розныя, дзеці розныя, універсальнага падыходу ў рабоце з імі быць не можа. Педагагічная работа заўсёды жывая і павінна мець зваротную сувязь, — упэўнена Таццяна Іванаўна. — Да кожнага ўрока трэба рыхтавацца, прадумваць сістэму заданняў, каб цікава і даступна выкладаць матэрыял, у тым ліку для слабых па ўзроўні навучанасці дзяцей. Калі ў некалькіх словах апісаць маю методыку работы, то я выкарыстоўваю дыферэнцыраваны падыход з элементамі актыўнай ацэнкі і модульнай тэхналогіі. Як гэта працуе? Я растлумачыла новую тэму. У канцы ўрока з мэтай рэфлексіі раздаю карткі, што змяшчаюць 5 заданняў на дзеянні, якія мы адпрацоўвалі на ўроку. Заданні не на адзнаку, а для таго, каб высветліць, чаму дзеці навучыліся. Пры падрыхтоўцы да наступнага ўрока я ўлічваю ўзровень разумення матэрыялу кожным вучнем. Той, хто навучыўся, зможа працаваць самастойна, а з астатнімі мне трэба будзе яшчэ раз замацаваць матэрыял. Вельмі патрабавальна я стаўлюся да ведання тэорыі, без яе — нікуды”.

Рабочая папка Таццяны Іванаўны запоўнена шматлікімі раздрукоўкамі, напісанымі ад рукі нататкамі, заданнямі на картках, якія прызначаны для работы з рознымі па здольнасцях да матэматыкі дзецьмі. На ўроках педагог не заўсёды паспявае адказаць на ўсе пытанні вучняў, праверыць заданні, якія дае індывідуальна, таму дзеці падыходзяць да яе на перапынках. Настаўніца заўсёды гаворыць вучням: “Вы можаце задаваць мне любыя пытанні, не бойцеся. Калі хтосьці не разумее, я растлумачу яшчэ раз. Наша агульная мэта — навучыцца”.

“Мой любімы выраз: калі робіш сваю справу, рабі добра або не рабі ўвогуле, — гаворыць Таццяна Іванаўна Рычак. — Сёння, як і 20 гадоў назад, калі я толькі пачынала сваю прафесійную дзейнасць, у мяне ёсць вялікае жаданне навучыць дзяцей матэматыцы. І пакуль я буду апантаная гэтай думкай, я змагу рухацца наперад у самаразвіцці, шукаць новыя метады і падыходы ў рабоце. Неверагоднае адчуванне, калі на тваіх вачах дзіця, якое не ведала, як рашаць матэматычную задачу, пачынае, дзякуючы табе, яе рашаць. Гэта сагравае душу і сэрца. Нібыта ты робіш глабальны ўклад у развіццё чалавецтва. Сваё значэнне ў гэтым свеце, сваю ролю ў грамадстве я адчуваю менавіта дзякуючы сваёй прафесіі”.

Надзея ЦЕРАХАВА.
Фота аўтара.